Transmitting messages meant converting the message into a sequence of symbols, The symbol or the sequence of symbols associated with a message is called the message code while the entire number of messages being transmitted might be called a message ensemble. The mutual agreement between the transmitter and the receiver about the meaning of the code for each message in the ensemble is called the ensemble code.
The concept of minimum redundancy code will be defined as the code used by a message ensemble consisting of a finite number of members N and for the given number of coding digits D yields the lowest possible average message length
This “Minimum Redundancy” or rather “Optimal” coding method had two rules
- No two messages will consist of an identical arrangement of coding digits
- No additional information would be needed to specify where the message code begins and ends once the starting point of a sequence of messages is known, this representation is called a prefix code.
The second rule or the prefix code is important because we are dealing with a variable-length encoding so there is a change of ambiguity, i.e we might not know where the encoding of one symbol ends and the other begins, but designing out encoding as a prefix code means that the bit string representing some particular symbol is never a prefix of the bit string representing any other symbol which means no ambiguity whatsoever
01, 102, 111, 202 is a valid prefix message code for an ensemble of four members, which means that
1111022020101111102 can be broken up without any ambiguity into
111-102-202-01-01-111-102
However, if the message code includes 11, 111, 102, and 02 then a 11 would result in ambiguity cause we will not know whether it corresponds to 11 or to 111
This rule forms the basis of Huffman Code an optimal algorithm for lossless data compression.
He proved his encoding as The most optimal way of assigning ones/zeros to a single character in his paper title A Method for the Construction of Minimum-Redundancy Codes which is the shortest paper I have ever read ! so quick shoutout to my man David for that.
Huffman coding turned the existing Shannon coding upside down and used a Bottoms up Approach i.e Merging from the leaves to the root to generate the tree.
Let’s suppose we need to encode A B C D and all of them equal probabilities of occurrence 1/4
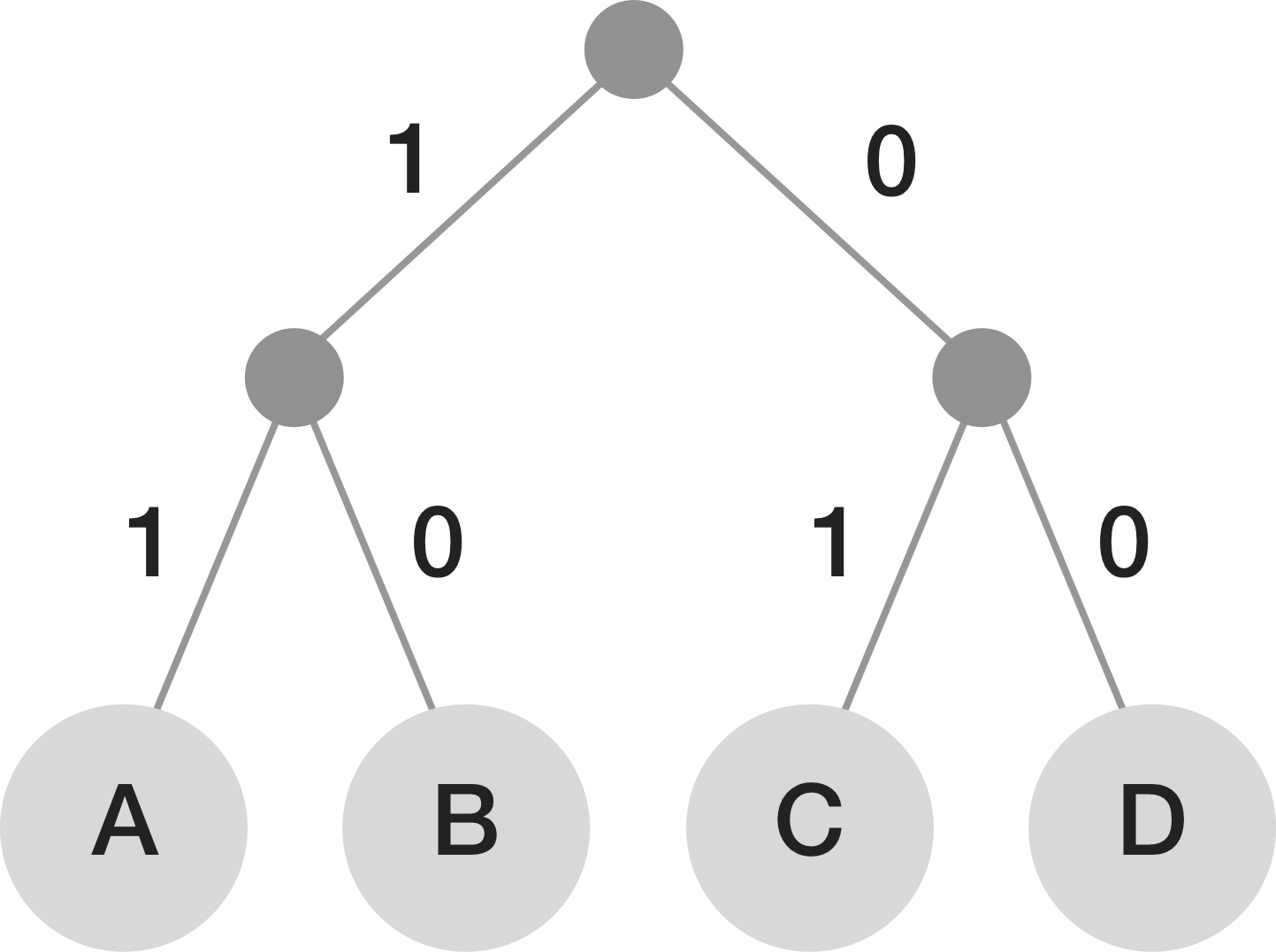
We generate a tree out of the probabilities such that the second level nodes sum up to 1/2 and the root node sums up to 1. We then use this tree to paint all the left nodes 1 and right nodes 0. Then the encodings are generate
A - 11
B - 10
C - 01
D - 00
Length = 2,2,2,2
Since the probabilities are the same the length of the code is always 2
Well now if we chose to point the left nodes as 0 and right nodes as 1 the coding we would be the reverse but will still end up being a prefix code and optimal.
Entropy of the code H = Σ Pi log(1/Pi) = 0.5+0.5+0.5+0.5 = 2
Expected code length = L = Σ pi Li = 4(1/4*2) = 2
Entropy (H)
Efficiency (E) = ━━━━━━━━━━━━━━━━━━━━
Expected Word length (L)
E = 2/2 = 1 ~ 100 percent :)
But this was easy cause the probabilities were all powers of 2 which might not always be the case
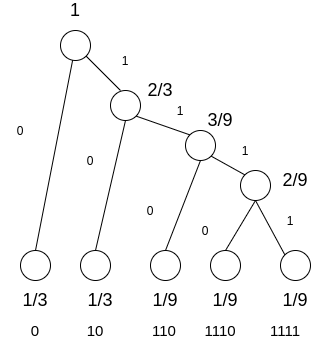
A - 0
B - 10
C - 110
D - 1110
E - 1111
Length = 1, 2, 3, 4, 4
In this above diagram, the probabilities are not powers of 2
Entropy of the code H = Σ Pi log(1/Pi)
= 2(1/3*log_2 (3)) + 3(1/9 * log_2 (9))
= 2.113
Expected code length = L = Σ pi Li
= (1/3 * 1) + (1/3 * 2) +(1/9 * 3) +(1/9 * 4) +(1/9 * 4)
= 2.222
Efficiency (E) = 2.113/ 2.222 = 0.95 ~ 95 Percent Efficiency
Here is the algorithm, For a given string of characters
- Calculate the frequency of each character in the string.
- Sort the characters in increasing order of the frequency
- Make each unique character as a leaf node.
- Create an empty node. Assign the minimum frequency as the left child and the second minimum frequency as the right child of the node.
- Assign the empty node a value that is the sum of the above two minimum frequencies.
- Repeat till we reach the maximum frequency character that would have a node one step away from the root node, which means the least number of bits to represent it.
The basic idea is to create a binary tree and operate on it in a bottoms-up manner so that the least two frequent characters are as far as possible from the root. In this way, the most frequent character gets the smallest code and the least frequent character gets the largest code.
Implementation
Huffman Coding can be implemented with a priority queue, Here is a rough pseudoscope
- Count the occurrences of each character in the string
- Place characters and counts into a priority queue
- Use priority queue to create Huffman tree
- Traverse the tree and assign right nodes 1 and left nodes 0
- Encode the string with the binary mapping
The Notebook visualizes the generated tree
https://github.com/sangarshanan/huffman-coding/blob/master/notebook.ipynb
Reference