Humans are not always awesome. we sometimes suck a lot, like during the world wars. While soldiers all around the world were fighting on the ground, the scientists were trying to figure out more effective means of getting information to them through popular communication signals like radio, telegraph and telephones (Propaganda was much more effective than the 3 combined)
The level of research and development in the communications–electronics field was unprecedented when scale and security became a major concern since war efforts were being controlled and coordinated using these communication channels. Communications were vital and so was intercepting and deciphering them. It was also during this time that Alan Turing broke the encryption of the Enigma machine used by Germans potentially ending the war and saving millions of lives.
In America an Emergency Technical Committee with members of Bell Labs was set up during the second world war and they proved instrumental in advancing Army and Navy ammunition acceptance and material sampling procedures. In 1943, Bell developed SIGSALY a secure system that made transmission of speech possible using pulse-code modulation. This was also the time when Alan Turing visited Bell labs representing the British and met Claude Shannon, a mathematician from Bell Labs to discuss the project and exchange ideas.
Even after the war ended the research and collaboration continued
Dawn of the Information Age
In 1948 Claude E. Shannon published an article in the Bell system technical journal called Mathematical Theory of Communication it quickly became one of the most cited of all scientific articles and gave rise to the field of Information Theory
In this paper Shannon laid out the general architecture of a communication system
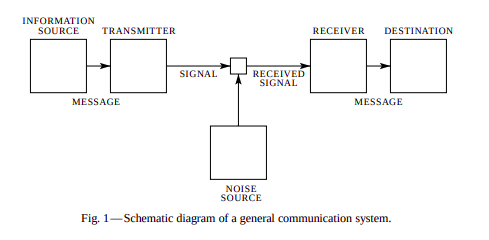
We start off with the Information Source that actually produces the message, then there is the transmitter that converts the message into a signal that would pass through a channel, perhaps even a noisy channel. After traversing the channel the signal reaches the receiver which would convert the signal back to the actual message that was sent to reach the destination.
We may roughly classify communication systems into three main categories: Discrete, Continuous or both. In discrete systems both the message and the signal are a sequence of discrete symbols i.e morse code while a continuous system treated both the message and signal as continuous functions like radio while a Mixed system would be a mix of both these systems
Discrete Communication Systems
The Morse code was slow and using a series of dashes and dots to communicate was never going to scale, The logical next step was to design a machine geared towards speed that would allow users to input these characters directly and then convert them to low-level signals for transmission.
These teleprinters were driven by some kind of clock just like how morse code was governed by time units. The Baudot system for example used 5 different keys that could represent two states (On/ Off) with this you were able to encode 2 * 2 * 2 * 2 * 2 = 32 characters using the 5 keys and these included the alphabets and some special characters like the space bar.

Shannon referred to the 5 different keys in the machine as Bits which we understand now but at the time was a new way of seeing the most fundamental unit of information.
Based on this we can conclude that our message space (Total number of possible messages) depends only on two things, the number of symbols transferred per second and the Number of bits we use to encode the symbols
N - Number of symbols transferred per second
S - Number of bits used to encode a symbol
Message Space = S ^ N
In Baudot system we use 2 bits and 5 different keys/symbols
that could be used so our message space = 2^5 = 16
The Message Space for many communication system can be though of like a tree
so for N=2 and S=2 we can visualize a tree like this where the leaf nodes are 00, 01, 10, 11
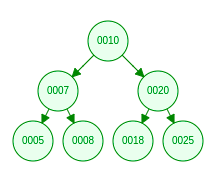
Using this we can also measure or quantify our information Number of bits
For example if we wanna send a 6 letter word with just zeros and ones, then we can do a binary search every time by splitting the 26 alphabets in half over iterations till we find the alphabet we want to find happens and this is nothing but the time complexity of a binary search algorithm which is Log2(26) and for a 6 letter word it will be 6 log2(26) = 28.20264 bits.
This was suggested as a practical measure of information by Henry Nyquist in the first section of his paper The Measurement of Information, whose work Shannon built upon
Information = N log(S) or log(S^N)
where S = number of symbols available at every selection(2) and N = Total number of symbols (26)
Here our transmission is constrained by the number of bits and the number of symbols, Suppose the system transmits n symbols per second it is natural to say that the channel has a capacity of 5n bits per second. This does not mean that the teletype channel will always be transmitting information at this rate and the actual rate depends on the source of information which feeds the channel. i.e the source can transmit really fast or really slow
What if we speed up the number of symbols per second ?
There are several issues when the symbols are fed too fast or even too slow.
- Signals coming in too fast can cause inter-signal interference
- Signals coming in too slow/interrupted by noise causes echoes/smoothing of these signals
So we need to maintain an optimal number of symbols per second for the receiver to decipher it.
Since these symbols are nothing but a combination of signals to decipher them we have the concept of time division i.e If a switch was on, it is impossible to turn it on again without turning it off, so we use time and record signals every second (time division is 1 sec) so every second we could measure the state to see if it is on or off. So light on for 2 continuous seconds would represent 1 1.
What if we bump the number of bits used to encode a symbol ?
We can easily observe one of the easiest way to speed up our transmission is to increase the channel capacity, by simply bumping 5 bits to 6 bits we can transmit 6n bits per second. Also instead of using each bit to represent one of two states we can represent multiple. This concept was successfully implemented in the Quadruplex telegraph where we did not just depend on On and Off but used signals of varying intensities and direction (+1,-1,+3,-3) to encode increase the number of messages which enabled us to send more messages without building new lines.
So why stop here why not encode a million different voltage levels per pulse and keep scaling, well we can’t ! Many different voltage resolutions means its that much harder for the receiver to decipher since signals will always be accompanied with noise
Noise in transmission is Unavoidable it can happen due to perfectly natural causes like heat or geomagnetic storms so the signals must be different enough to be unaltered by noise.
The introduction of noisy channels was one of the key additions that Shannon made to the earlier work of Nyquist and Hartley while working on his communication model
Information Entropy
This uncertainty or noise because of natural phenomenon correlates with our understanding of entropy in statistical mechanics.
The basic intuition behind information theory is that learning that an unlikely event has occurred is more informative than learning that a likely event has occurred. This means when quantifying information we must also deal with surprise or the events that have a low probability of occurrence
We can calculate the amount of information there is in an event using the probability of the event.
Shannon Information = -log(P(X))
This is an adaptation of what Nyquist presented + the Noise factor hence its a probability.
So P(X) is the probability of the event x. We use the - just to be sure the value is positive, This information will be zero when the probability of an event is 1 or a certainty i.e there is no surprise.
Low probability events are more surprising and carry more information, and the complement of high probability events carry less information.
These were the old timey days so transmitting bits across long distances was not really cheap so we wanted to answer a fundamental question What is the Least number of bits I encode a given information ? and this was the measure of information and what a person who wants to transmit a message will be charged based on.
This Information can be also presented as The minimum number of questions we can ask
With the Coin toss the Information is 1 since we only need to ask 1 question, Heads or Tails Now if we consider a dice roll then what would be the minimum number of these questions
Let’s assume that a random roll had lead us to 5
1 2 3 4 5 6
1) Is the number lesser than 3 - No
3 4 5 6
2) Is the number lesser than 5 - No
5 6
3) Is the number lesser than 6 - YES
5
So here we asked 3 questions and if the number was 1 we would have required just 2 questions
And of course from the formula Information = log_2(1/6) = 2.585 bits
We can now derive entropy from this Information, The intuition for entropy is that it is the average number of bits required to represent or transmit an event drawn from the probability distribution for the random variable. In other words it is the average level of “information”, “surprise”, or “uncertainty” inherent in the variable’s possible outcomes
Entropy = - Σ p(x) log(p(x))
In the coin toss all events are equally possible so we can never place our bets on anything cause everything is Likely and this is the truest state of entropy just like the universe.
The largest entropy for a random variable will be if all events are equally likely
In the case where one event dominates, such as a skewed probability distribution there is less surprise and the distribution will have a lower entropy. In the case where no event dominates another, such as equal or approximately equal probability distribution, then we would expect larger or maximum entropy.
For a skewed distribution, lets take a coin toss where Heads is 90 % more likely than tails
Entropy = -(9/10 * log(9/10) + 1/10 * log(1/10)) = 0.46899559358
Which is much lower than when the probability is 1/2
which would give us an entropy of 1
Entropy = -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1
Lesser the entropy lesser the number of questions we can ask before guessing the outcome
This unit of entropy is a bit which can now be used as a Measure of Surprise or as a Quantitative Measure of Information.
Now that we know how to quantify the minimum number of questions or bits needed to describe our data or rather the information entropy it can be used for a lot of things though the most direct applications are in Data Compression and Error Correction.
Shannon-Fano Coding
Shannon posited that if entropy increases then our ability to compress decreases and vice versa and if we wanna compress beyond out entropy then it needs to be lossy. In his paper he presented his technique for compression which draws from Fanos method
Around 1948, both Claude E. Shannon (1948) and Robert M. Fano (1949) independently proposed two different source coding algorithms for an efficient description of a discrete memoryless source. Unfortunately, in spite of being different, both schemes became known under the same name Shannon–Fano coding.
Lets consider the alphabets A,B,C,D,E with the given occurrences and probabilities based on it
| Symbol | Count | Probability |
| A | 15 | 15 / 39 |
| B | 7 | 7 / 39 |
| C | 6 | 6 / 39 |
| D | 6 | 6 / 39 |
| E | 5 | 5 / 39 |
With Shannon code we calculate the word lengths of each of these letter based on entropy
word length = - log(p(x))
We can pick codewords in order, choosing the lexicographically first word of the correct length that maintains the prefix-free property. Clearly A gets the codeword 00. To maintain the prefix-free property, B’s codeword may not start 00, so the lexicographically first available word of length 3 is 010. Continuing like this, we get the following code:
| Symbol | A | B | C | D | E |
|---|---|---|---|---|---|
| Probabilities p(i) | 0.385 | 0.179 | 0.154 | 0.154 | 0.128 |
| Word length -log2(p(i)) | 2 | 3 | 3 | 3 | 3 |
| Codewords | 00 | 010 | 011 | 100 | 101 |
Avg Length = 2 Bits * (15) + 3 bits * (7 + 6 + 6 + 5) / 39 = 2.62 Bits per symbol
The Fano code is constructed as follows: the source messages a(i) and their probabilities p( a(i) ) are listed in order of nonincreasing probability. This list is then divided in such a way as to form two groups of as nearly equal total probabilities as possible. Each message in the first group receives 0 as the first digit of its codeword; the messages in the second half have codewords beginning with 1. Each of these groups is then divided according to the same criterion and additional code digits are appended. The process is continued until each subset contains only one message.
To minimize the difference we start by dividing this list into A and BCDE with this division, A and B will each have a code that starts with a 0 bit, and the C, D, and E codes will all start with a 1. Subsequently, the left half of the tree gets a new division between A and B, which puts A on a leaf with code 00 and B on a leaf with code 01.
After four division procedures, a tree of codes results. In the final tree, the three symbols with the highest frequencies have all been assigned 2-bit codes, and two symbols with lower counts have 3-bit codes as shown table below:
| Symbol | A | B | C | D | E |
|---|---|---|---|---|---|
| Probabilities | 0.385 | 0.179 | 0.154 | 0.154 | 0.128 |
| First Division | 0 | 0 | 1 | 1 | 1 |
| Second Division | 0 | 1 | 0 | 1 | 1 |
| Third Division | 0 | 1 | |||
| Codewords | 00 | 01 | 10 | 110 | 111 |
Avg Length = 2 Bits * (15 + 7 + 6) + 3 bits * (6 + 5) / 39 = 2.28 Bits per symbol
We see that Fano’s method, with an average length of 2.28, has outperformed Shannon’s method, with an average length of 2.62.
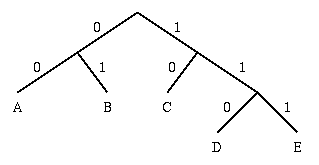
Tree is generated by Dividing from the root to the leaves i.e Top Down Approach
This encoding produces fairly efficient variable-length encodings when we can partition our initial set to two smaller sets of equal probability but in cases where can’t achieve this the encoding is not guaranteed to produce optimal codes
We can also the split divide the list in different way and depending on what we choose there may be two different codes for the same symbol so loss of data means we need to start from scratch.
Now there is an another way to do this, a more optimal way. It was presented in 1952 by David Huffman in his paper called A Method for the Construction of Minimum-Redundancy Codes
Huffman coding turned the existing shannon coding upside down and used a Bottoms up Approach i.e Merging from the leaves to the root to generate the tree.
cOoL tHinGs
Information theory got soo huge in the scientific community after this paper with people from different fields and interests jumping in and getting their hands dirty that Claude Shannon wrote a follow up paper called
The Bandwagonhttps://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=1056774
Claude Shannon was born in Gaylord :) Yes I am seven
Stolen from
- http://people.math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf
- https://www.khanacademy.org/computing/computer-science/informationtheory#moderninfotheory
- https://www.ics.uci.edu/~dan/pubs/DC-Sec3.html
- https://en.wikipedia.org/wiki/Shannon%E2%80%93Fano_coding
- http://compression.ru/download/articles/huff/huffman_1952_minimum-redundancy-codes.pdf