Algorithms that make me cry: Hamming Codes
So I recently came across the impossible chessboard puzzle on 3Blue1Brown
tl;dr of the puzzle, So we have a checkerboard with coins placed in a random order of heads and tails and a prize under one of the boards. Now by only disturbing a single piece on the board we should indicate the position of the prize to our teammate with whom we can collude with beforehand.
This problem is a solid, battle tested way to lose friends at parties.
At first glance it seems super crazy, there is no way you can alter just one coin to indicate a position when you have so many choices and combinations in front of you, its hard to properly understand the problem at this scale, so like a cute little engineer you break it down to a much smaller problem
Lets say we have two board, the combinations possible are
[H H], [T T], [H T], [T H]
Here is the rule: If the first coin is Head its under the first board or its on the second board
easy peasy right, now lets add to the combination and try to visualize this with 3 coins
This is where the video gets better cause to understand this problem properly at a higher dimension visualization is the key. we can represent the 4 combinations previously presented as a square where the two opposite sides indicate the two positions the key can reside, 3B1B beautifully illustrates this in 3D and goes onto explain why it would actually not work for combination that are not a power of 2, also how you can elegantly scale the solution from 2 boards to 64 boards.
The underlying algorithm is something that we actually use in our daily life, oh this is where the beautiful error correction algorithms come in, When we have information encoded as a combination of 1s and 0s passing through a noisy channel there is a high possibility that a few get flipped and we must be able to identify these flipped bits without any knowledge on the initial state.
Now there are several error correction algorithms ranging in complexities and efficiency, some of the popular ones include Hamming codes, BCH codes, Reed solomen codes and so on, we can gonna explore hamming codes.
I learnt about hamming codes in college, I did not find them remotely interesting nor did I bother learning more about them, bless the wonders of university education.
Again 3B1B made two excellent videos illustrating hamming codes the hardware and the software
tl;dr of the videos
Hamming codes uses the concept of parity bits, so it have 256 bits then we use 9 out of those bits √256 + 1 to encode information about the rest of the bits and if anything flips we can refer to those to identify the exact block, Now scale down and look at 16 block for which we need 5 parity
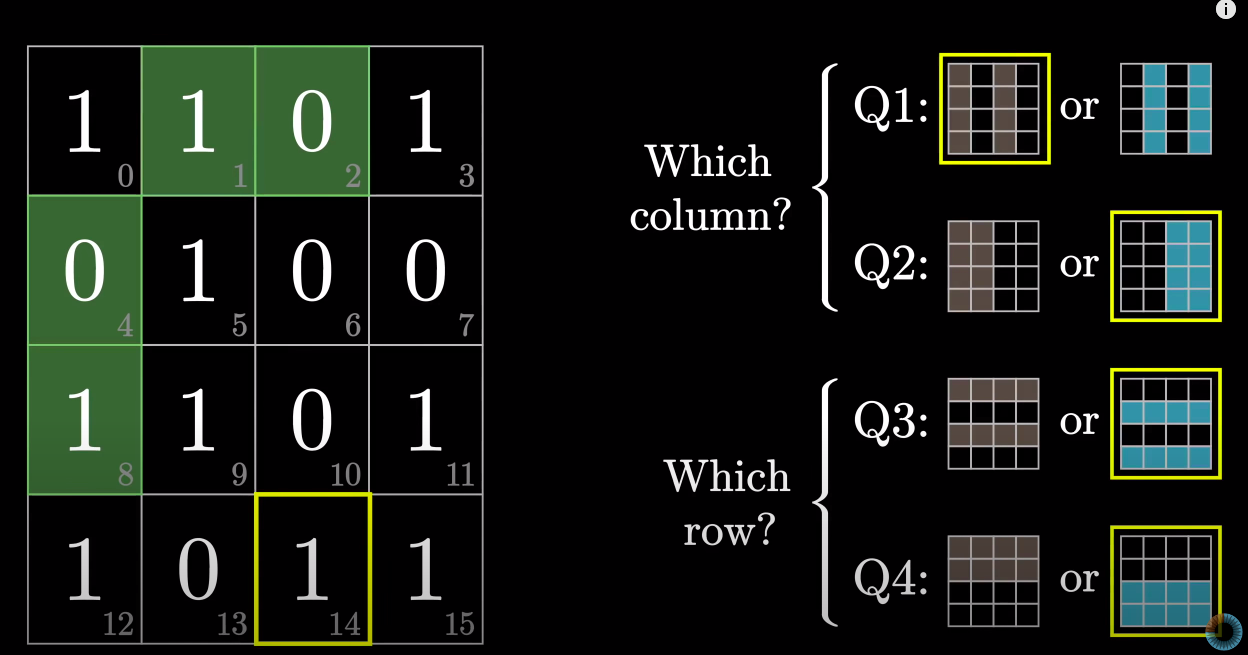
The 4 parity bits are colored in green and the other parity bit would be the 0th bit (Global parity)
These 4 parity bits answer 2 important questions, the Row ? and the Column ? of the error
For example in the image above the error is on bit 14,
So the parity checks would have passed at Q1 [C2,C4] failed at Q2 [C2, C3] which means that the error is at C3 or the 3rd column. Similarly check fails at Q3 which means [R2, R4] and also fails at Q4 which means [R4, R5] so the intersection row is R4 or the error is on the 4th Row
Hence C3 R4 = 14th bit, So we can deduce that it is the noise bit
There is a clear flaw, What happens when more than one bits get inverted, This where hamming codes kinda fail. But we have a 0th bit that we can use to store the parity of the whole block
-
If we find out there is an error -> Parity of the whole block changed => Just one error
-
If we find out there is an error -> but parity of the whole block is unchanged => Two errors
Pretty neat but we still dont know where those two bits are, lets leave that to Reed Solomen

When represented in binary we observe something interesting, the four questions that we asked the groups that decided the row and column can be translated to a binary form just as easily based on the position of 1 in the binary form of the bit
Also notice how each parity bit only sit inside one and only one of the 4 parity groups, the fact that every parity group needs just one parity bit ensures that we can scale in powers of 2 (the 256 bit board needed only 9 parity bits)
Also here is another doozy, lets look the heads and tail problem we solved with 2 coins
If both the coins are the same (H,H) or (T,T) we say the coin is under first bit and if either one of the bits is different (H,T) ot (T,H) we say it is under board 2, sound familiar ?
Ok so if two bits are the same we return a 0 and if any one of those bits flip we return 1 ???
Tis the Goddamn XOR gate !!
The second video explains how the whole parity calculation is just an XOR(), it just blows my mind every time and this definitely is why this algorithms make me cry everytime I think about it.
Here is the whole algorithm in basically two points
- So if we have (10101) then we flip some bits such that XOR(1^0^1^0^1) return 0
- Now if one of those bits get flipped in transit then the XOR(1^1^0^1^0) of the noisy bunch is no longer 0 but is the exact index of the position of the bit that was flipped
How freaking awesome is that !
I tried converting this algorithm into code that “kinda works”
In today’s edition “I could never come up with something like this” we decided to stan hamming codes
:wq